Notes
two overlapping semi-circles solution
Two Overlapping Semi-Circles
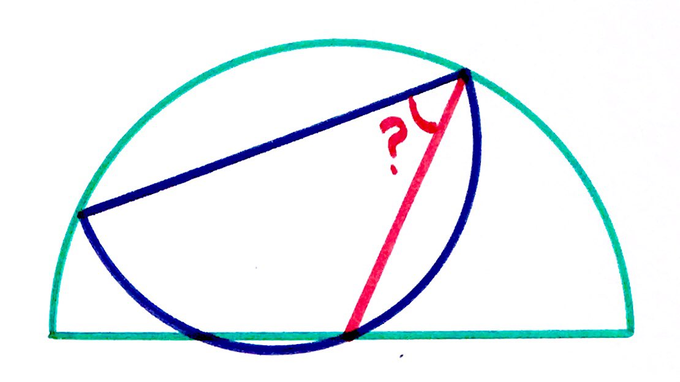
The larger semicircle has twice the area of the smaller one. What’s the angle?
Solution by Chord Properties and Pythagoras' Theorem
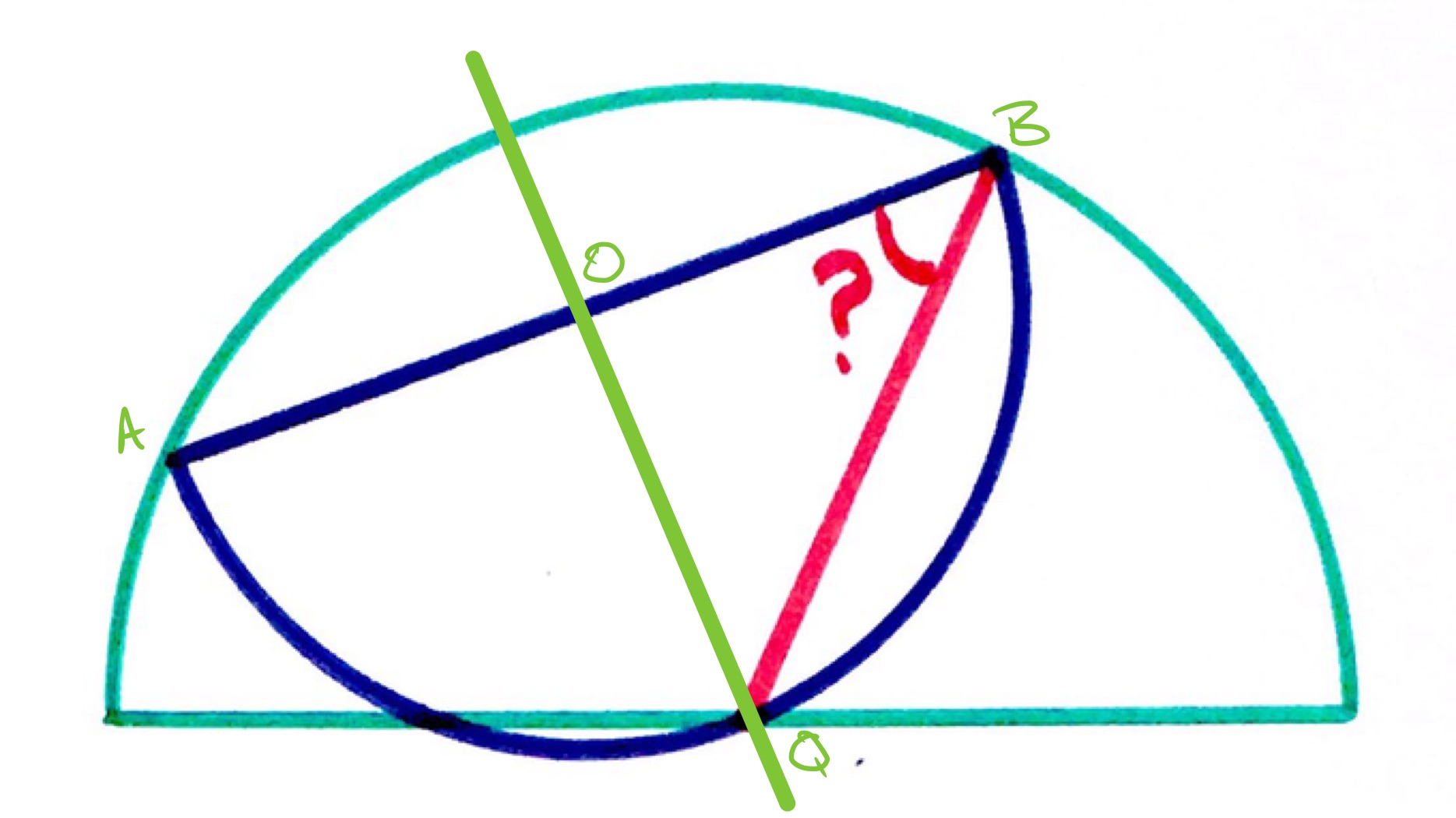
In the above diagram, is the centre of the smaller semi-circle and so is the midpoint of the chord . The point is one of the points where the smaller semi-circle intersects with the diameter of the larger one.
Consider the following diagram, in which is the centre of the larger semi-circle.
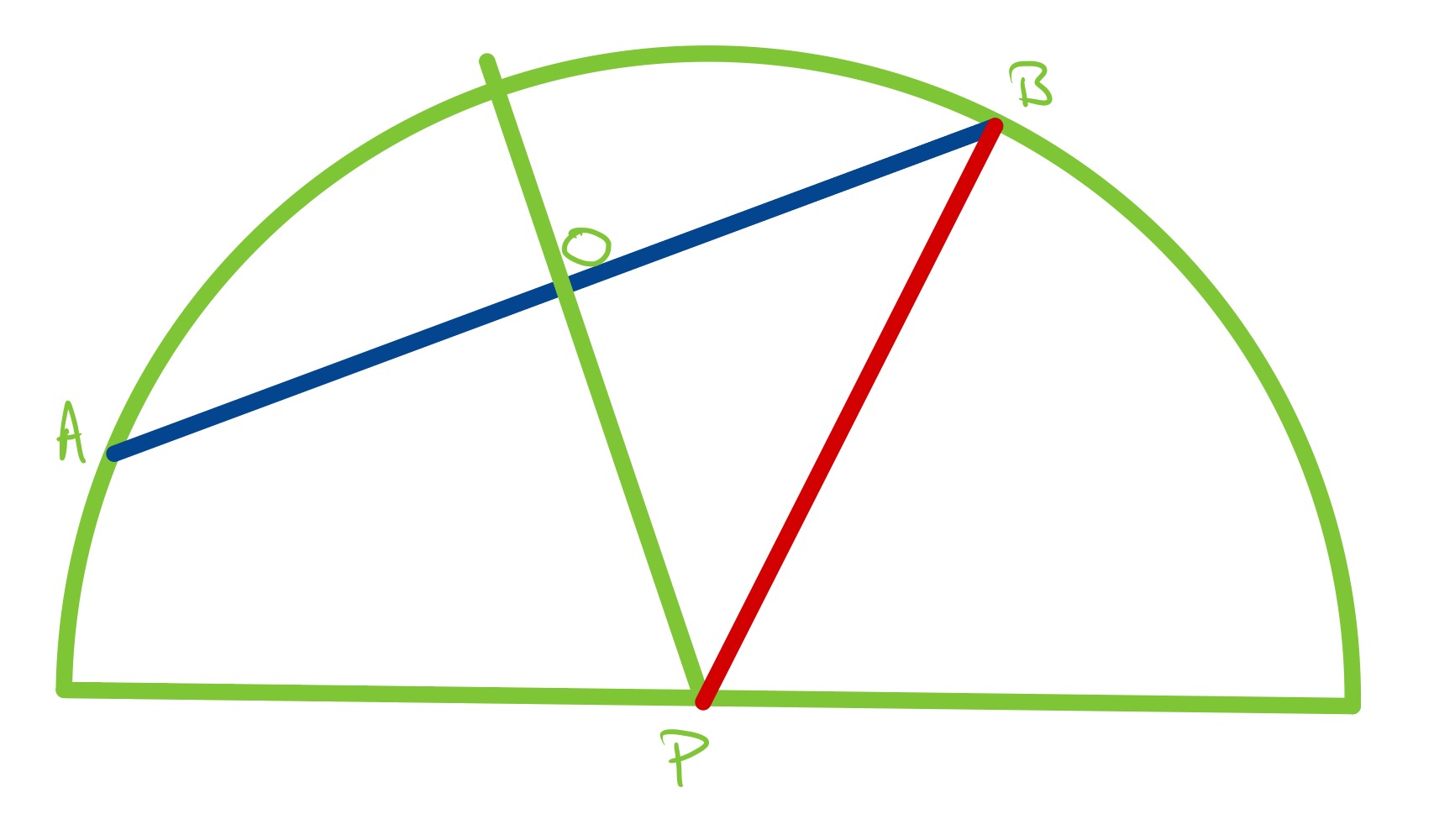
As is a chord of the larger circle and is its midpoint, the line is perpendicular to . Let , , be the lengths of , , and respectively. Then is the radius of the smaller semi-circle and of the larger. Since the larger has twice the area of the smaller, so . Triangle is a right-angled triangle so from Pythagoras' theorem, which leads to and hence (as both are lengths), .
This means that point is a distance from and so also lies on the smaller semi-circle. This shows that of this diagram and in the earlier diagram are actually the same point, so triangle is an isosceles right-angled triangle and hence angle is .